T1
链接:6171. 和相等的子数组
难度:Easy
给你一个下标从
0开始的整数数组nums,判断是否存在两个长度为2的子数组且它们的和相等。注意,这两个子数组起始位置的下标必须不相同。如果这样的子数组存在,请返回true,否则返回false。
子数组是一个数组中一段连续非空的元素组成的序列。
数据范围:
- $2 \leq nums.length \leq 1000$
- $-10^9 \leq nums[i] \leq 10^9$
示例 1:
输入: nums = [4,2,4]
输出: true
解释: 元素为 [4,2] 和 [2,4] 的子数组有相同的和 6 。
示例 2:
输入: nums = [1,2,3,4,5]
输出: false
解释: 没有长度为 2 的两个子数组和相等。
示例 3:
输入: nums = [0,0,0]
输出: true
解释: 子数组 [nums[0],nums[1]] 和 [nums[1],nums[2]] 的和相等,都为 0 。
注意即使子数组的元素相同,这两个子数组也视为不相同的子数组,因为它们在原数组中的起始位置不同。
分析
比较的是长度为2的子数组,一个长度为n的数组最多只有n-1个长度为2的子数组,直接枚举即可。枚举过程中用一个哈希表维护已经出现过的和
时间复杂度
一次遍历,$O(n)$
实现
class Solution {
public:
bool findSubarrays(vector<int>& nums) {
unordered_set<int> s;
for (int i = 0; i < nums.size() - 1; i++) {
int t = nums[i] + nums[i + 1];
if (s.count(t)) return true;
s.insert(t);
}
return false;
}
};T2
链接:6172. 严格回文的数字
难度:Medium
如果一个整数
n在b进制下(b 为 2 到 n - 2 之间的所有整数)对应的字符串全部都是 回文的,那么我们称这个数n是严格回文的。给你一个整数n,如果n是严格回文的,请返回true,否则返回false。
如果一个字符串从前往后读和从后往前读完全相同,那么这个字符串是回文的。
数据范围:
- $4 \leq n \leq 10^5$
示例1:
输入:n = 9
输出:false
解释:在 2 进制下:9 = 1001 ,是回文的。
在 3 进制下:9 = 100 ,不是回文的。
所以,9 不是严格回文数字,我们返回 false 。
注意在 4, 5, 6 和 7 进制下,n = 9 都不是回文的。
示例2:
输入:n = 4
输出:false
解释:我们只考虑 2 进制:4 = 100 ,不是回文的。
所以我们返回 false 。
分析
直接按照题意模拟。对于一个输入n,枚举2到n-2之间的所有数x,把n转换为x进制数,判断是否回文
时间复杂度
枚举2到n-2之前的数x,复杂度为$O(n)$。对于每一个x,把n转换为x进制数,复杂度为$O(log_xn)$。因为$x \geq 2$,所以$log_xn \leq log_2n$,总体复杂度为$O(nlogn)$
实现
class Solution {
public:
bool isStrictlyPalindromic(int n) {
for (int i = 2; i <= n - 2; i++) {
if (!check(n, i)) return false;
}
return true;
}
bool check(int x, int i) {
vector<int> s;
while (x) {
s.push_back(x % i);
x /= i;
}
for (int i = 0, j = s.size() - 1; i < j; i++, j--) {
if (s[i] != s[j]) return false;
}
return true;
}
};T3
链接:6173. 被列覆盖的最多行数
难度:Medium
给你一个下标从
0开始的m x n二进制矩阵mat和一个整数cols,表示你需要选出的列数。如果一行中,所有的1都被你选中的列所覆盖,那么我们称这一行被覆盖了。
请你返回在选择cols列的情况下被覆盖的行数最大为多少。
数据范围
- $ m == mat.length $
- $ n == mat[i].length $
- $ 1 \leq m, n \leq 12 $
- $ mat[i][j] $ 要么是$0$要么是$1$
- $ 1 \leq cols \leq n $
示例1: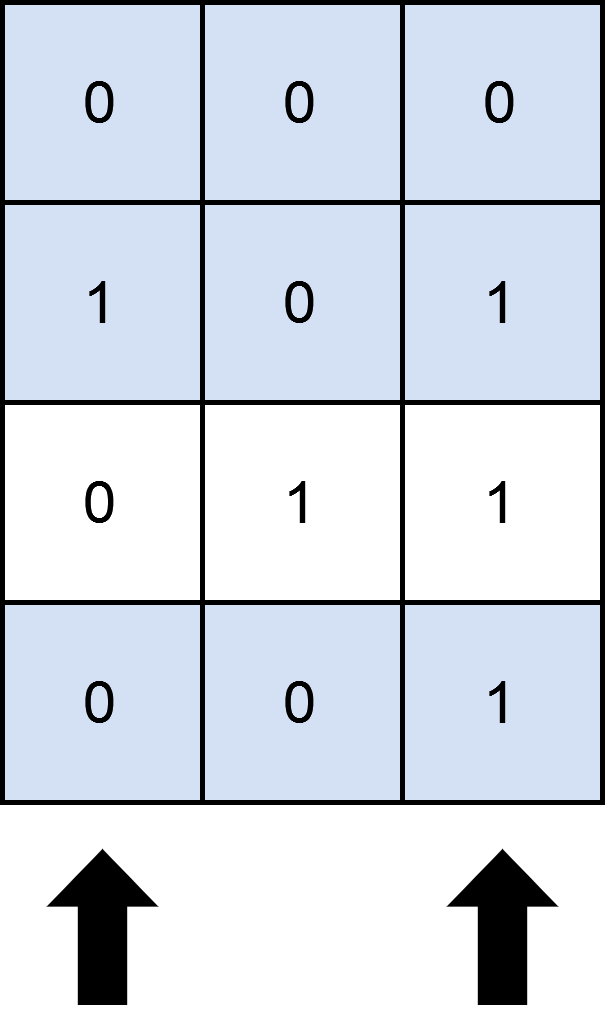
输入:mat = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], cols = 2
输出:3
解释:
如上图所示,覆盖 3 行的一种可行办法是选择第 0 和第 2 列。
可以看出,不存在大于 3 行被覆盖的方案,所以我们返回 3 。
示例2:
输入:mat = [[1],[0]], cols = 1
输出:2
解释:
选择唯一的一列,两行都被覆盖了,原因是整个矩阵都被覆盖了。
所以我们返回 2 。
分析
本题数据范围很小,直接枚举所有选法取最大覆盖行数即可
枚举策略:本题的输入可以看作是m个n位的二进制数S;选中某一列视为该位置1,不选置0,这样一个选法也唯一对应了一个二进制数x。一个选法可以覆盖某行,当且仅当该行所表示的数S & x = S,即该行中所有为1的列都在选法中被选择了
选法直接二进制枚举,从$0$到$2^n$。如果数x中1的个数不等于cols,说明是个无效选法,直接跳过
时间复杂度
枚举选法$2^n$
实现
class Solution {
public:
int maximumRows(vector<vector<int>>& mat, int cols) {
int m = mat.size(), n = mat[0].size();
vector<int> s(m);
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
s[i] |= mat[i][j] << j;
}
}
int res = 0;
for (int x = 0; x < 1 << n; x++) {
if (cnt(x) != cols) continue;
int t = 0;
for (int i = 0; i < m; i++) {
if ((s[i] & x) == s[i]) t++;
}
res = max(res, t);
}
return res;
}
int cnt(int x) {
int res = 0;
while (x) {
res += x & 1;
x >>= 1;
}
return res;
}
};T4
链接:6143. 预算内的最多机器人数目
难度:Hard
你有
n个机器人,给你两个下标从0开始的整数数组chargeTimes和runningCosts,两者长度都为n。第i个机器人充电时间为chargeTimes[i]单位时间,花费runningCosts[i]单位时间运行。再给你一个整数budget。运行k个机器人总开销是max(chargeTimes) + k * sum(runningCosts),其中max(chargeTimes)是这k个机器人中最大充电时间,sum(runningCosts)是这k个机器人的运行时间之和。
请你返回在不超过budget的前提下,你最多可以连续运行的机器人数目为多少。
数据范围:
- $ chargeTimes.length == runningCosts.length == n $
- $ 1 \leq n \leq 5 \times 10^4 $
- $ 1 \leq chargeTimes[i], runningCosts[i] \leq 10^5 $
- $ 1 \leq budget \leq 10^{15} $
示例1:
输入:chargeTimes = [3,6,1,3,4], runningCosts = [2,1,3,4,5], budget = 25
输出:3
解释:
可以在 budget 以内运行所有单个机器人或者连续运行 2 个机器人。
选择前 3 个机器人,可以得到答案最大值 3 。总开销是 max(3,6,1) + 3 sum(2,1,3) = 6 + 3 6 = 24 ,小于 25 。
可以看出无法在 budget 以内连续运行超过 3 个机器人,所以我们返回 3 。
示例2:
输入:chargeTimes = [11,12,19], runningCosts = [10,8,7], budget = 19
输出:0
解释:即使运行任何一个单个机器人,还是会超出 budget,所以我们返回 0 。
分析
本题的中文翻译略微有一点小问题,「可以连续运行的机器人」中连续指的是下标连续,即我们的答案一定是某一个子数组而不是子序列
暴力思路
我们可以从大到小枚举长度,在每个长度下再枚举区间,直接计算总开销,第一个符合要求的长度即为答案。在枚举区间时,可以用单调队列维护max(chargeTimes),用前缀和求sum(runningCosts)。但是,这样总体的时间复杂度为$O(n^2)$,会超时,需要进一步优化
二分答案
我们的暴力做法中第一层枚举了所有的区间长度,如果可以优化就可以降低复杂度。注意到我们的答案是满足限制的最大长度,假设答案为ans,对于所有大于ans的长度都不存在一个子数组满足限制,所有小于等于ans的长度,至少存在一个子数组满足限制(可以把ans对应的子数组从一边去掉一些元素),而ans正好是两者的边界。所以,我们可以用二分在[0, n]中搜索答案。这样时间复杂度为$O(nlogn)$
双指针
在枚举区间的过程中可以发现:对于一个给定的区间,随着右端点向右移动,总开销是单调递增的(max(chargeTimes) + k * sum(runningCosts),添加一个数max不会变小;runningCosts都是正数,添加一个数sum也不会变小,同时k变大)。所以,如果已知一个右端点r对应的满足限制的最左端点为l,那么对于r+1,其对应的满足限制的最左端点至少为l。即:随着右端点不断向右,其对应的最左端点也在不断向右,两个指针的变化具有单调性。
思路:从小到大枚举所有右端点r,分别求出满足限制的最左端点l,此时区间长度为r-l+1,答案即为最长的一个。由于枚举过程是单调的,可以用单调队列维护max(chargeTimes),用一个临时变量维护sum(runningCosts),时间复杂度$O(n)$
时间复杂度
$O(n)$
实现
typedef long long LL;
class Solution {
public:
int maximumRobots(vector<int>& chargeTimes, vector<int>& runningCosts, long long budget) {
int res = 0;
deque<int> q;
LL sum = 0ll;
for (int i = 0, j = 0; i < chargeTimes.size(); i++) {
while (q.size() && chargeTimes[q.back()] <= chargeTimes[i]) q.pop_back();
q.push_back(i);
sum += runningCosts[i];
while (q.size() && chargeTimes[q.front()] + (i - j + 1) * sum > budget) {
if (q.front() == j) q.pop_front();
sum -= runningCosts[j++];
}
res = max(res, i - j + 1);
}
return res;
}
};